Poisson MLE via Homomorphic Computation
Introduction
We present a toy example of a homomorphic computation involving maximum likelihood estimation.
Consider the following data motivated by an example from the mle function in the stats4 R package: we wish to estimate \(\lambda\), the Poisson parameter \(\lambda\) for randomly generated count data y below:
library(stats4)
set.seed(17822)
y <- rpois(n = 40, lambda=10)
# Easy one-dimensional MLE:
nLL <- function(lambda) -sum(stats::dpois(y, lambda, log = TRUE))
fit0 <- mle(nLL, start = list(lambda = 5), nobs = NROW(y))The function nLL is the negative log-likelihood of the data and the function mle computes the maximum likelihood estimate that can be printed out.
summary(fit0)## Maximum likelihood estimation
##
## Call:
## mle(minuslogl = nLL, start = list(lambda = 5), nobs = NROW(y))
##
## Coefficients:
## Estimate Std. Error
## lambda 9.175 0.4789311
##
## -2 log L: 199.5328logLik(fit0)## 'log Lik.' -99.76641 (df=1)Distributed Computation
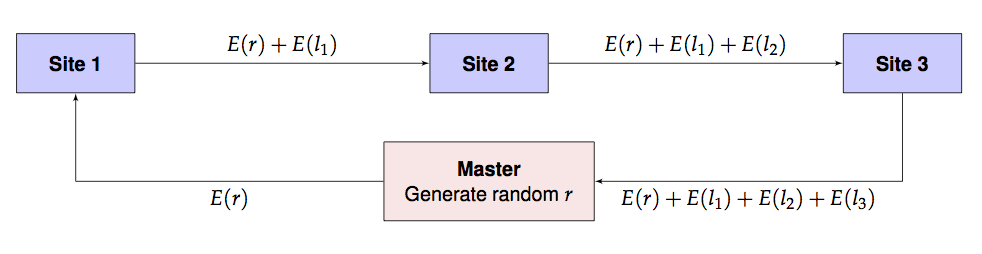
Assume now that the data y is distributed between three sites, none of whom want to share actual data among each other or even with a master computation process. They wish to keep their data secret but are willing, together, to provide the sum of their local negative log-likelihoods. They need to do this in a way so that the master process will not be able to associate the contribution to the likelihood from each site. To simulate this, let’s partition the data y as follows.
y1 <- y[1:20]
y2 <- y[21:27]
y3 <- y[28:40]The overall likelihood function \(l(\lambda)\) for the entire data is therefore the sum of the likelihoods at each site: \(l(\lambda) = l_1(\lambda)+l_2(\lambda)+l_3(\lambda).\) How can this likelihood be computed while maintaining privacy?
Assuming that every site including the master has access to a homomorphic computation library such as homomorpheR, the likelihood can be computed in a privacy-preserving manner using the following scheme. We use \(E(x)\) and \(D(x)\) to denote the encrypted and decrypted values of \(x\) respectively.
- Master generates a public/private key pair. Master distributes the public key to all sites. (The private key is not distributed and kept only by the master.)
- Master generates a random offset \(r\) to obfuscate the intial likelihood.
- Master sends \(E(r)\) and a guess \(\lambda_0\) to site 1. Note that \(\lambda\) is not encrypted.
- Site 1 computes \(l_1 = l(\lambda_0, y_1)\), the local likelihood for local data \(y_1\) using parameter \(\lambda_0\). It then sends on \(\lambda_0\) and \(E(r) + E(l_1)\) to site 2.
- Site 2 computes \(l_2 = l(\lambda_0, y_2)\), the local likelihood for local data \(y_2\) using parameter \(\lambda_0\). It then sends on \(\lambda_0\) and \(E(r) + E(l_1) + E(l_2)\) to site 3.
- Site 3 computes \(l_3 = l(\lambda_0, y_3)\), the local likelihood for local data \(y_3\) using parameter \(\lambda_0\). It then sends on \(E(r) + E(l_1) + E(l_2) + E(l_3)\) back to master.
- Master retrieves \(E(r) + E(l_1) + E(l_2) + E(l_3)\) which, due to the homomorphism, is exactly \(E(r+l_1+l_2+l_3) = E(r+l).\) So the master computes \(D(E(r+l)) - r\) to obtain the value of the overall likelihood at \(\lambda_0\).
- Master updates \(\lambda_0\) with a new guess \(\lambda_1\) and repeats steps 1-5. This process is iterated to convergence. For added security, even steps 0-5 can be repeated, at additional computational cost.
This is pictorially shown below.
Implementation
The above implementation assumes that the encryption and decryption can happen with real numbers which is not the actual situation. Instead, we use rational approximations using a large denominator, \(2^{256}\), say. In the future, of course, we need to build an actual library is built with rigorous algorithms guaranteeing precision and overflow/undeflow detection. For now, this is just an ad hoc implementation.
Also, since we are only using homomorphic additive properties, a partial homomorphic scheme such as the Paillier Encryption system will be sufficient for our computations.
We define a class to encapsulate our sites that will compute the Poisson likelihood on site data given a parameter \(\lambda\). Note how the addNLLAndForward method takes care to split the result into an integer and fractional part while performing the arithmetic operations. (The latter is approximated by a rational number.)
library(gmp)
library(homomorpheR)
Site <- R6::R6Class("Site",
private = list(
## name of the site
name = NA,
## only master has this, NA for workers
privkey = NA,
## local data
data = NA,
## The next site in the communication: NA for master
nextSite = NA,
## is this the master site?
iAmMaster = FALSE,
## intermediate result variable
intermediateResult = NA
),
public = list(
## Common denominator for approximate real arithmetic
den = NA,
## The public key; everyone has this
pubkey = NA,
initialize = function(name, data, den) {
private$name <- name
private$data <- data
self$den <- den
},
setPublicKey = function(pubkey) {
self$pubkey <- pubkey
},
setPrivateKey = function(privkey) {
private$privkey <- privkey
},
## Make me master
makeMeMaster = function() {
private$iAmMaster <- TRUE
},
## add neg log lik and forward to next site
addNLLAndForward = function(lambda, enc.offset) {
if (private$iAmMaster) {
## We are master, so don't forward
## Just store intermediate result and return
private$intermediateResult <- enc.offset
} else {
## We are workers, so add and forward
## add negative log likelihood and forward result to next site
## Note that offset is encrypted
nllValue <- self$nLL(lambda)
result.int <- floor(nllValue)
result.frac <- nllValue - result.int
result.fracnum <- as.bigq(numerator(as.bigq(result.frac) * self$den))
pubkey <- self$pubkey
enc.result.int <- pubkey$encrypt(result.int)
enc.result.fracnum <- pubkey$encrypt(result.fracnum)
result <- list(int = pubkey$add(enc.result.int, enc.offset$int),
frac = pubkey$add(enc.result.fracnum, enc.offset$frac))
private$nextSite$addNLLAndForward(lambda, enc.offset = result)
}
## Return a TRUE result for now.
TRUE
},
## Set the next site in the communication graph
setNextSite = function(nextSite) {
private$nextSite <- nextSite
},
## The negative log likelihood
nLL = function(lambda) {
if (private$iAmMaster) {
## We're master, so need to get result from sites
## 1. Generate a random offset and encrypt it
pubkey <- self$pubkey
offset <- list(int = random.bigz(nBits = 256),
frac = random.bigz(nBits = 256))
enc.offset <- list(int = pubkey$encrypt(offset$int),
frac = pubkey$encrypt(offset$frac))
## 2. Send off to next site
throwaway <- private$nextSite$addNLLAndForward(lambda, enc.offset)
## 3. When the call returns, the result will be in
## the field intermediateResult, so decrypt that.
sum <- private$intermediateResult
privkey <- private$privkey
intResult <- as.double(privkey$decrypt(sum$int) - offset$int)
fracResult <- as.double(as.bigq(privkey$decrypt(sum$frac) - offset$frac) / den)
intResult + fracResult
} else {
## We're worker, so compute local nLL
-sum(stats::dpois(private$data, lambda, log = TRUE))
}
})
)We are now ready to use our sites in the computation.
1. Generate public and private key pair
We also choose a denominator for all our rational approximations.
keys <- PaillierKeyPair$new(1024) ## Generate new public and private key.
den <- gmp::as.bigq(2)^256 #Our denominator for rational approximations2. Create sites
site1 <- Site$new(name = "Site 1", data = y1, den = den)
site2 <- Site$new(name = "Site 2", data = y2, den = den)
site3 <- Site$new(name = "Site 3", data = y3, den = den)The master process is also a site but has no data. So has to be thus designated.
## Master has no data!
master <- Site$new(name = "Master", data = c(), den = den)
master$makeMeMaster()2. Distribute public key to sites
site1$setPublicKey(keys$pubkey)
site2$setPublicKey(keys$pubkey)
site3$setPublicKey(keys$pubkey)
master$setPublicKey(keys$pubkey)Only master has private key for decryption.
master$setPrivateKey(keys$getPrivateKey())3. Define the communication graph
Master will always send to the first site, and then the others have to forward results in turn with the last site returning to the master.
master$setNextSite(site1)
site1$setNextSite(site2)
site2$setNextSite(site3)
site3$setNextSite(master)4. Perform the likelihood estimation
fit1 <- mle(master$nLL, start = list(lambda = 5))Print the summary.
summary(fit1)## Maximum likelihood estimation
##
## Call:
## mle(minuslogl = master$nLL, start = list(lambda = 5))
##
## Coefficients:
## Estimate Std. Error
## lambda 9.175 0.4789311
##
## -2 log L: 199.5328logLik(fit1)## 'log Lik.' -99.76641 (df=1)The results should be the same as above.
Applications via distcomp and opencpu
One can imagine these sort of computations being constructed within the framework described the R package distcomp where the sites are opencpu servers and there is a master process executing the computation. Much work remains to be done to make this work in a seamless manner; however, as this proof-of-concept example shows, the technical hurdles are quite surmountable.
CAVEAT
This is an initial proof-of-concept implementation that has to substantially improved for real-world use. You’ve been warned.